Overview#
A quantify-core experiment typically consists of a data-acquisition loop in
which one or more parameters are set and one or more parameters are measured.
The core of Quantify can be understood by understanding the following concepts:
Code snippets#
Instruments and Parameters#
Parameter#
A parameter represents a state variable of the system. Parameters:
can be gettable and/or settable;
contain metadata such as units and labels;
are commonly implemented using the QCoDeS
Parameterclass.
A parameter implemented using the QCoDeS Parameter class
is a valid Settable and Gettable and as such can be used directly in
an experiment loop in the MeasurementControl (see subsequent sections).
Instrument#
An Instrument is a container for parameters that typically (but not necessarily) corresponds to a physical piece of hardware.
Instruments provide the following functionality:
Container for parameters.
A standardized interface.
Logging of parameters through the
snapshot()method.
All instruments inherit from the QCoDeS Instrument class.
They are displayed by default in the InstrumentMonitor
Measurement Control#
The MeasurementControl (meas_ctrl) is in charge of the data-acquisition loop
and is based on the notion that, in general, an experiment consists of the following
three steps:
Initialize (set) some parameter(s),
Measure (get) some parameter(s),
Store the data.
quantify-core provides two helper classes, Settable and Gettable to aid
in these steps, which are explored further in later sections of this article.
MeasurementControl provides the following functionality:
standardization of experiments;
standardization data storage;
\(n\)-dimensional sweeps;
data acquisition controlled iteratively or in batches;
adaptive sweeps (measurement points are not predetermined at the beginning of an experiment).
Basic example, a 1D iterative measurement loop#
Running an experiment is simple! Simply define what parameters to set, and get, and what points to loop over.
In the example below we want to set frequencies on a microwave source and acquire the signal from the Qblox Pulsar readout module:
meas_ctrl.settables(
mw_source1.freq
) # We want to set the frequency of a microwave source
meas_ctrl.setpoints(np.arange(5e9, 5.2e9, 100e3)) # Scan around 5.1 GHz
meas_ctrl.gettables(pulsar_QRM.signal) # acquire the signal from the pulsar QRM
dset = meas_ctrl.run(name="Frequency sweep") # run the experiment
Starting iterative measurement...
The MeasurementControl can also be used to perform more advanced experiments
such as 2D scans, pulse-sequences where the hardware is in control of the acquisition
loop, or adaptive experiments in which it is not known what data points to acquire in
advance, they are determined dynamically during the experiment.
Take a look at some of the tutorial notebooks for more in-depth examples on
usage and application.
Control Mode#
Batched mode can be used to deal with constraints imposed by (hardware) resources or to reduce overhead.
In iterative mode , the measurement control steps through each setpoint one at a time, processing them one by one.
In batched mode , the measurement control vectorizes the setpoints such that they are processed in batches. The size of these batches is automatically calculated but usually dependent on resource constraints; you may have a device that can hold 100 samples but you wish to sweep over 2000 points.
Note
The maximum batch size of the settable(s)/gettable(s) should be specified using the
.batch_size attribute. If not specified infinite size is assumed and all setpoint
are passed to the settable(s).
Tip
In Batched mode it is still possible to perform outer iterative sweeps with an inner
batched sweep.
This is performed automatically when batched settables (.batched=True) are mixed
with iterative settables (.batched=False). To correctly grid the points in this mode
use MeasurementControl.setpoints_grid().
Control mode is detected automatically based on the .batched attribute of the
settable(s) and gettable(s); this is expanded upon in subsequent sections.
Note
All gettables must have the same value for the .batched attribute.
Only when all gettables have .batched=True, settables are allowed to have mixed
.batched attribute (e.g. settable_A.batched=True, settable_B.batched=False).
Depending on which control mode the MeasurementControl is running in,
the interfaces for Settables (their input interface) and Gettables
(their output interface) are slightly different.
It is also possible for batched gettables to return an array with a length less than the length of the setpoints, and similarly for the input of the Settables. This is often the case when working with resource-constrained devices, for example, if you have n setpoints but your device can load only less than n datapoints into memory. In this scenario, measurement control tracks how many datapoints were actually processed, automatically adjusting the size of the next batch.
Settables and Gettables#
Experiments typically involve varying some parameters and reading others.
In quantify-core we encapsulate these concepts as the Settable
and Gettable respectively.
As their name implies, a Settable is a parameter you set values to,
and a Gettable is a parameter you get values from.
The interfaces for Settable and Gettable parameters are encapsulated in the
Settable and Gettable helper classes respectively.
We set values to Settables; these values populate an X-axis.
Similarly, we get values from Gettables which populate a Y-axis.
These classes define a set of mandatory and optional attributes the
MeasurementControl recognizes and will use as part of the experiment,
which are expanded up in the API reference.
For ease of use, we do not require users to inherit from a Gettable/Settable class,
and instead provide contracts in the form of JSON schemas to which these classes
must fit (see Settable and Gettable docs for these schemas).
In addition to using a library that fits these contracts
(such as the Parameter family of classes).
we can define our own Settables and Gettables.
t = ManualParameter("time", label="Time", unit="s")
class WaveGettable:
"""An examples of a gettable."""
def __init__(self):
self.unit = "V"
self.label = "Amplitude"
self.name = "sine"
def get(self):
"""Return the gettable value."""
return np.sin(t() / np.pi)
def prepare(self) -> None:
"""Optional methods to prepare can be left undefined."""
print("Preparing the WaveGettable for acquisition.")
def finish(self) -> None:
"""Optional methods to finish can be left undefined."""
print("Finishing WaveGettable to wrap up the experiment.")
# verify compliance with the Gettable format
wave_gettable = WaveGettable()
Gettable(wave_gettable)
“Grouped” gettable(s) are also allowed. Below we create a Gettable which returns two distinct quantities at once:
t = ManualParameter(
"time",
label="Time",
unit="s",
vals=validators.Numbers(), # accepts a single number, e.g. a float or integer
)
class DualWave1D:
"""Example of a "dual" gettable."""
def __init__(self):
self.unit = ["V", "V"]
self.label = ["Sine Amplitude", "Cosine Amplitude"]
self.name = ["sin", "cos"]
def get(self):
"""Return the value of the gettable."""
return np.array([np.sin(t() / np.pi), np.cos(t() / np.pi)])
# N.B. the optional prepare and finish methods are omitted in this Gettable.
# verify compliance with the Gettable format
wave_gettable = DualWave1D()
Gettable(wave_gettable)
.batched and .batch_size#
The Gettable and Settable objects can have a bool property
.batched (defaults to False if not present); and an int property .batch_size.
Setting the .batched property to True enables the batched control code*
in the MeasurementControl. In this mode, if present,
the .batch_size attribute is used to determine the maximum size of a batch of
setpoints, that can be set.
Heterogeneous batch size and effective batch size
The minimum .batch_size among all settables and gettables will determine the
(maximum) size of a batch.
During execution of a measurement the size of a batch will be reduced if necessary
to comply to the setpoints grid and/or total number of setpoints.
.prepare() and .finish()#
Optionally the .prepare() and .finish() can be added.
These methods can be used to set up and teardown work.
For example, arming a piece of hardware with data and then closing a connection upon
completion.
The .finish() runs once at the end of an experiment.
For settables, .prepare() runs once before the start of a measurement.
For batched gettables, .prepare() runs before the measurement of each batch.
For iterative gettables, the .prepare() runs before each loop counting towards
soft-averages [controlled by meas_ctrl.soft_avg() which resets to 1
at the end of each experiment].
Data storage#
Along with the produced dataset, every Parameter
attached to QCoDeS Instrument in an experiment run through
the MeasurementControl of Quantify is stored in the [snapshot].
This is intended to aid with reproducibility, as settings from a past experiment can
easily be reloaded [see load_settings_onto_instrument()].
Data Directory#
The top-level directory in the file system where output is saved to.
This directory can be controlled using the get_datadir()
and set_datadir() functions.
We recommend changing the default directory when starting the python kernel
(after importing quantify_core) and settling for a single common data directory
for all notebooks/experiments within your measurement setup/PC
(e.g., D:\\quantify-data).
quantify-core provides utilities to find/search and extract data,
which expects all your experiment containers to be located within the same directory
(under the corresponding date subdirectory).
Within the data directory experiments are first grouped by date -
all experiments which take place on a certain date will be saved together in a
subdirectory in the form YYYYmmDD.
Experiment Container#
Individual experiments are saved to their own subdirectories (of the Data Directory)
named based on the TUID and the
<experiment name (if any)>.
Note
TUID: A Time-based Unique ID is of the form
YYYYmmDD-HHMMSS-sss-<random 6 character string> and these subdirectories’
names take the form
YYYYmmDD-HHMMSS-sss-<random 6 character string><-experiment name (if any)>.
These subdirectories are termed ‘Experiment Containers’, with a typical output being the Dataset in hdf5 format and a JSON format file describing Parameters, Instruments and such.
Furthermore, additional analyses such as fits can also be written to this directory, storing all data in one location.
An experiment container within a data directory with the name "quantify-data"
thus will look similar to:
quantify-data/
├── 20210301/
├── 20210428/
└── 20230125/
└── 20230125-172802-085-874812-my experiment/
├── analysis_BasicAnalysis/
│ ├── dataset_processed.hdf5
│ ├── figs_mpl/
│ │ ├── Line plot x0-y0.png
│ │ ├── Line plot x0-y0.svg
│ │ ├── Line plot x1-y0.png
│ │ └── Line plot x1-y0.svg
│ └── quantities_of_interest.json
└── dataset.hdf5
Dataset#
The Dataset is implemented with a specific convention using the
xarray.Dataset class.
quantify-core arranges data along two types of axes: X and Y.
In each dataset there will be n X-type axes and m Y-type axes.
For example, the dataset produced in an experiment where we sweep 2 parameters (settables)
and measure 3 other parameters (all 3 returned by a Gettable),
we will have n = 2 and m = 3.
Each X axis represents a dimension of the setpoints provided.
The Y axes represent the output of the Gettable.
Each axis type are numbered ascending from 0
(e.g. x0, x1, y0, y1, y2),
and each stores information described by the Settable and Gettable
classes, such as titles and units.
The Dataset object also stores some further metadata,
such as the TUID of the experiment which it was
generated from.
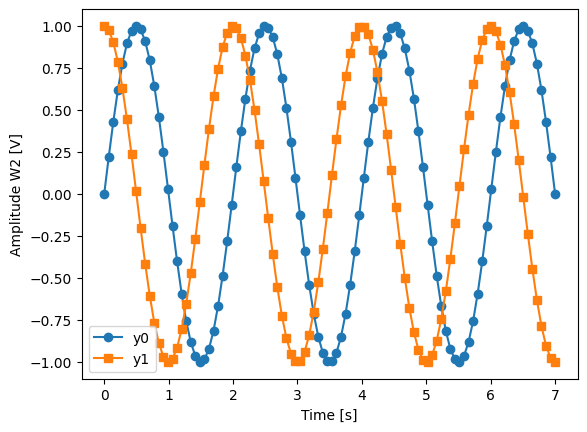
For example, consider an experiment varying time and amplitude against a Cosine function. The resulting dataset will look similar to the following:
# plot the columns of the dataset
_, axs = plt.subplots(3, 1, sharex=True)
xr.plot.line(quantify_dataset.x0[:54], label="x0", ax=axs[0], marker=".")
xr.plot.line(quantify_dataset.x1[:54], label="x1", ax=axs[1], color="C1", marker=".")
xr.plot.line(quantify_dataset.y0[:54], label="y0", ax=axs[2], color="C2", marker=".")
tuple(ax.legend() for ax in axs)
# return the dataset
quantify_dataset
<xarray.Dataset> Size: 24kB
Dimensions: (dim_0: 1000)
Coordinates:
x0 (dim_0) float64 8kB -1.0 -0.7778 -0.5556 ... 0.5556 0.7778 1.0
x1 (dim_0) float64 8kB 0.0 0.0 0.0 0.0 0.0 ... 10.0 10.0 10.0 10.0
Dimensions without coordinates: dim_0
Data variables:
y0 (dim_0) float64 8kB -1.0 -0.7778 -0.5556 ... -0.6526 -0.8391
Attributes:
tuid: 20250904-041044-620-001ca8
name: my experiment
grid_2d: True
grid_2d_uniformly_spaced: True
xlen: 10
ylen: 100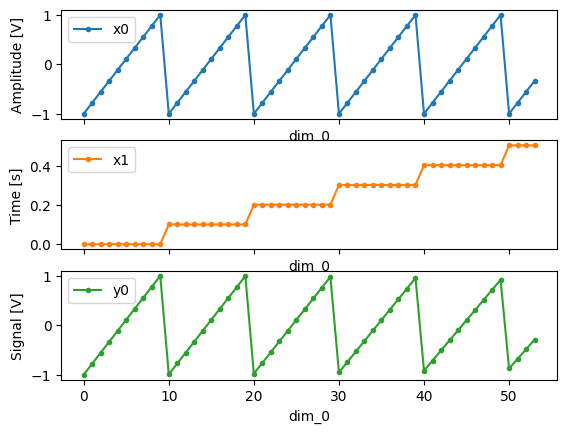
Associating dimensions to coordinates#
To support both gridded and non-gridded data, we use Xarray
using only Data Variables and Coordinates with a single Dimension
(corresponding to the order of the setpoints).
This is necessary as in the non-gridded case the dataset will be a perfect sparse array, the usability of which is cumbersome. A prominent example of non-gridded use-cases can be found Tutorial 4. Adaptive Measurements.
To allow for some of Xarray’s more advanced functionality,
such as the in-built graphing or query system we provide a dataset conversion utility
to_gridded_dataset().
This function reshapes the data and associates dimensions to the dataset
[which can also be used for 1D datasets].
gridded_dset = dh.to_gridded_dataset(quantify_dataset)
gridded_dset.y0.plot()
gridded_dset
<xarray.Dataset> Size: 9kB
Dimensions: (x0: 10, x1: 100)
Coordinates:
* x0 (x0) float64 80B -1.0 -0.7778 -0.5556 -0.3333 ... 0.5556 0.7778 1.0
* x1 (x1) float64 800B 0.0 0.101 0.202 0.303 ... 9.697 9.798 9.899 10.0
Data variables:
y0 (x0, x1) float64 8kB -1.0 -0.9949 -0.9797 ... -0.8897 -0.8391
Attributes:
tuid: 20250904-041044-620-001ca8
name: my experiment
grid_2d: False
grid_2d_uniformly_spaced: True
xlen: 10
ylen: 100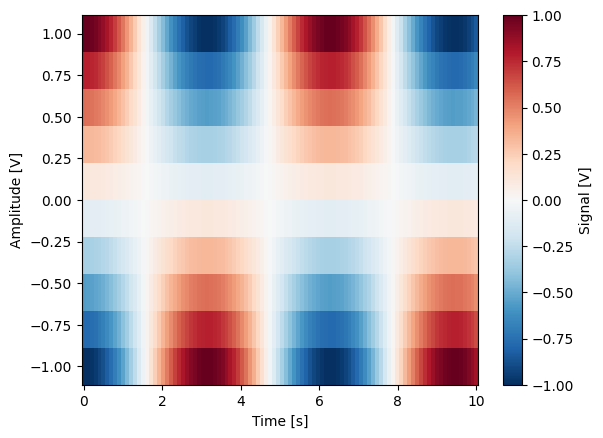
Snapshot#
The configuration for each QCoDeS Instrument
used in this experiment.
This information is automatically collected for all Instruments in use.
It is useful for quickly reconstructing a complex set-up or verifying that
Parameter objects are as expected.
Analysis#
To aid with data analysis, quantify comes with an analysis module
containing a base data-analysis class
(BaseAnalysis)
that is intended to serve as a template for analysis scripts
and several standard analyses such as
the BasicAnalysis,
the Basic2DAnalysis
and the ResonatorSpectroscopyAnalysis.
The idea behind the analysis class is that most analyses follow a common structure consisting of steps such as data extraction, data processing, fitting to some model, creating figures, and saving the analysis results.
To showcase the analysis usage we generate a dataset that we would like to analyze.
Using an analysis class#
Running an analysis is very simple:
a_obj = ca.CosineAnalysis(label="Cosine experiment")
a_obj.run() # execute the analysis.
a_obj.display_figs_mpl() # displays the figures created in previous step.
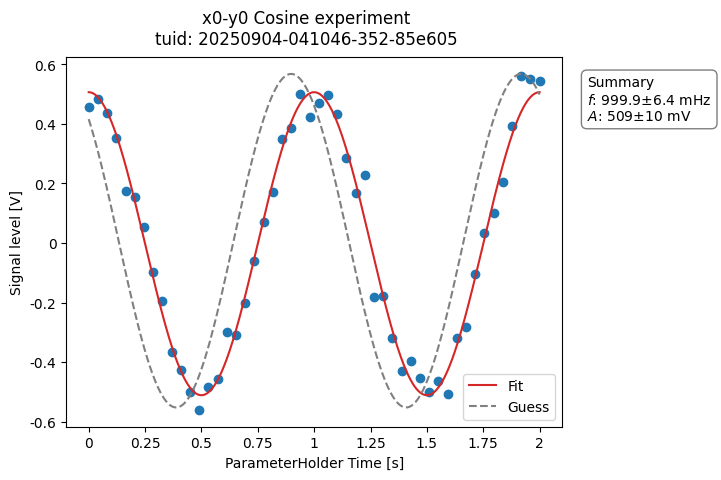
The analysis was executed against the last dataset that has the label
"Cosine experiment" in the filename.
After the analysis the experiment container will look similar to the following:
20230125-172804-537-f4f73e-Cosine experiment/
├── analysis_CosineAnalysis/
│ ├── dataset_processed.hdf5
│ ├── figs_mpl/
│ │ ├── cos_fit.png
│ │ └── cos_fit.svg
│ ├── fit_results/
│ │ └── cosine.txt
│ └── quantities_of_interest.json
├── dataset.hdf5
└── snapshot.json
The analysis object contains several useful methods and attributes such as the
quantities_of_interest, intended to store relevant quantities extracted
during analysis, and the processed dataset.
For example, the fitted frequency and amplitude are saved as:
freq = a_obj.quantities_of_interest["frequency"]
amp = a_obj.quantities_of_interest["amplitude"]
print(f"frequency {freq}")
print(f"amplitude {amp}")
frequency 1.000+/-0.006
amplitude 0.509+/-0.010
The use of these methods and attributes is described in more detail in Tutorial 3. Building custom analyses - the data analysis framework.
Creating a custom analysis class#
The analysis steps and their order of execution are determined by the
analysis_steps attribute
as an Enum (AnalysisSteps).
The corresponding steps are implemented as methods of the analysis class.
An analysis class inheriting from the abstract-base-class
(BaseAnalysis)
will only have to implement those methods that are unique to the custom analysis.
Additionally, if required, a customized analysis flow can be specified by assigning it
to the analysis_steps attribute.
The simplest example of an analysis class is the
BasicAnalysis
that only implements the
create_figures() method
and relies on the base class for data extraction and saving of the figures.
Take a look at the source code (also available in the API reference):
A slightly more complex use case is the
ResonatorSpectroscopyAnalysis
that implements
process_data()
to cast the data to a complex-valued array,
run_fitting()
where a fit is performed using a model
(from the quantify_core.analysis.fitting_models library), and
create_figures()
where the data and the fitted curve are plotted together.
Creating a custom analysis for a particular type of dataset is showcased in the Tutorial 3. Building custom analyses - the data analysis framework. There you will also learn some other capabilities of the analysis and practical productivity tips.
Examples: Settables and Gettables#
Below we give several examples of experiments that use Settables and Gettables in different control modes.
Iterative control mode#
Single-float-valued settable(s) and gettable(s)#
Each settable accepts a single float value.
Gettables return a single float value.
For more dimensions, you only need to pass more settables and the corresponding setpoints.
Single-float-valued settable(s) with multiple float-valued gettable(s)#
Each settable accepts a single float value.
Gettables return a 1D array of floats, with each element corresponding to a different Y dimension.
We exemplify a 2D case, however, there is no limitation on the number of settables.
Batched control mode#
Float-valued array settable(s) and gettable(s)#
Each settable accepts a 1D array of float values corresponding to all setpoints for a single X dimension.
Gettables return a 1D array of float values with each element corresponding to a datapoint in a single Y dimension.
Mixing iterative and batched settables#
In this case:
One or more settables accept a 1D array of float values corresponding to all setpoints for the corresponding X dimension.
One or more settables accept a float value corresponding to its X dimension.
Measurement control will set the value of each of these iterative settables before each batch.
Float-valued array settable(s) with multi-return float-valued array gettable(s)#
Each settable accepts a 1D array of float values corresponding to all setpoints for a single X dimension.
Gettables return a 2D array of float values with each row representing a different Y dimension, i.e. each column is a datapoint corresponding to each setpoint.